OPERAÇÃO ENTRE CONJUNTOS

 Existem algumas operações que podem ser realizadas entre conjuntos, são elas: intersecção, união e diferença.

Considerando os conjuntos A e B contidos num conjunto universo U, as operações entre eles podem ser representadas da seguinte maneira:

Intersecção 

A intersecção de A com B é o conjunto formado pelos elementos comuns a A e B.

Notação A ∩ B. (o que tem nos dois)

A ∩ B = {x / x Є A e x Є B}

União

A união de A com B é o conjunto formado por todos os elementos pertencentes a A ou a B.

Notação A U B. (membros dos dois conjuntos)

A U B = {x / x Є A ou x Є B}

Diferença 

A diferença entre A e B é o conjunto formado pelos elementos que pertencem a A e não pertencem a B.

Notação A – B. (o que tem em A e não tem em B)

A – B = {x / x Є A e x não pertence a B}

Exemplo 1

Sendo A = {1, 2, 3, 4} e B = {2, 4, 6}

A ∩ B = {2, 4}

A U B = {1, 2, 3, 4, 6}

A – B = {1, 3}

B – A = {6}

Exemplo 2

Sendo A = {1, 2, 3, 4, 5, 6, 7, 8, 9} e B = {10, 11, 12, 13, 14, 15}

A ∩ B = Ø (conjunto vazio)

A U B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}

A – B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

B – A = {10, 11, 12, 13, 14, 15}

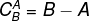
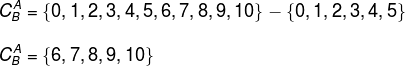
Conjuntos complementares

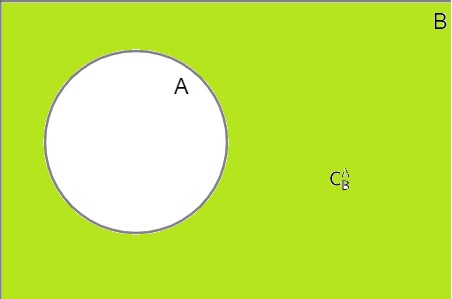
Considere os conjuntos A e B, em que o conjunto A está contido  (está dentro) no conjunto B, isto é, todo elemento de A também é elemento de B. A diferença entre os conjuntos, B – A, é chamada de complementar de A em relação a B. Em outras palavras, o complementar é formado por todo elemento que não pertence ao conjunto A em relação ao conjunto B, em que ele está contido.

Exemplo

Considere os conjuntos A = {0, 1, 2, 3, 4, 5} e B ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

O complementar de A em relação a B é:

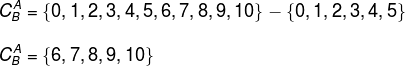
EXERCÍCIOS

1 Considere os conjuntos A = {a, b, c, d, e, f} e B ={d, e, f, g, h, i}. Determine (A – B) U (B – A).

2 Suponhamos que A U B = {a, b, c, d, e, f, g, h}, A ∩ B = {d, e} e A – B = {a, b, c}, então:

a) B = {f, g, h}

b) B = {d, e, f, g, h}

c) B = { }

d) B = {d, e}

e) B = {a, b, c, d, e}

GABARITO

1 {a, b, c, g, h, i}

2 b